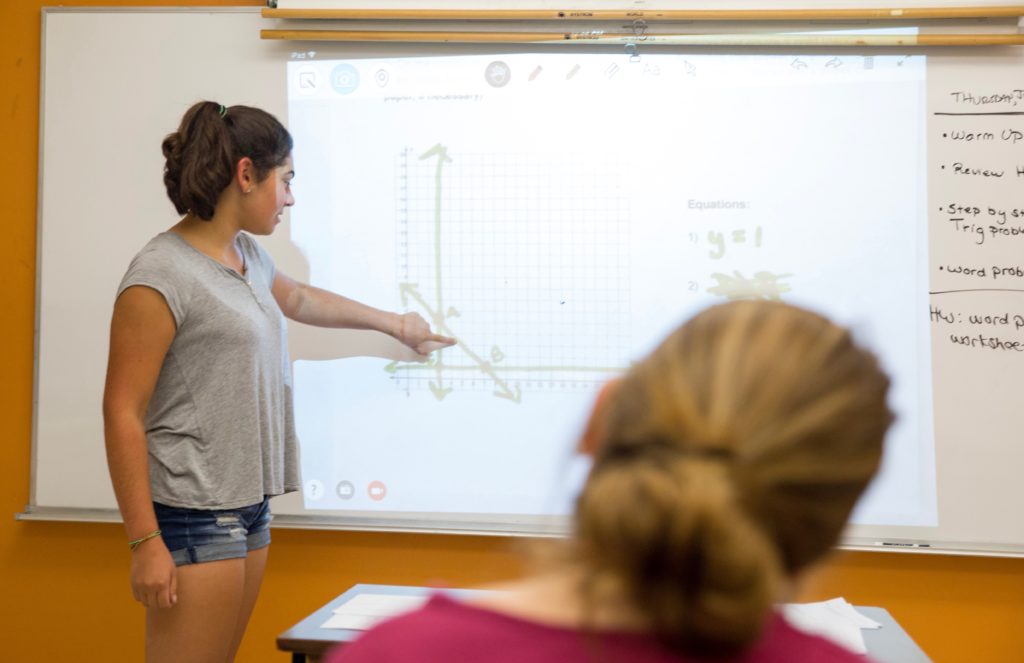Resources

Developing Number Sense with Number Strings

By Avery McNiff

April 14, 2021

What are Number Strings?

A number string is a series of carefully structured and related math problems that develop an understanding of number relationships and operations (Fosnot & Dolk, 2001). The practice engages students in problem solving and provides opportunities for students to participate in math discourse. 

Number strings are a flexible, adaptable, and short (15-20 minutes) activity that can serve as a daily warm up with whole classes or small groups. Teachers can design number strings around a range of mathematical topics, from addition to algebra.  

Number Strings in Practice

A small group of fifth grade students gather around a table. The teacher begins the lesson by asking students to brainstorm strategies they know for multiplication. One student shares, “counting by 10s, 5s, any number,” which the teacher labels as skip counting. They review repeated addition (e.g., 5 + 5 + 5 = 5×3), doubling (e.g., 3×10 = 2 x (3×5)  = 3×5+3×5), and arrays. Arrays are a model consisting of rows and columns that can be used to explore and understand properties of multiplication and division. A student adds, “breaking it down,” which is a newer strategy for the group and also the focus of the day’s number string. The teacher has designed this particular string around “breaking it down,” or the distributive property, and uses arrays, a familiar model to these students, to represent the strategy. 

After the initial brainstorm, the teacher writes the first problem on the board.

3×5

“Give me a thumb’s up when you have it,” the teacher says before providing ample wait time for students to think. 

After everyone has a “quiet thumb,” the teacher calls on students to share an answer, prompting them to explain their strategy or build off of the strategies of others. Students solved the problem by skip counting by 3, skip counting by 5, and repeated addition. The teacher represents their thinking on the board by drawing a closed 3×5 array. She uses the image to illustrate the idea of skip counting (3,6,9,12,15 or 5,10,15) and repeated addition (5+5+5 or 3+3+3+3+3). 

Next, the teacher writes the following helper problem, which builds upon the first, highlights doubling, sets up a conversation around place value, and serves as an anchor for illustrating the distributive property:

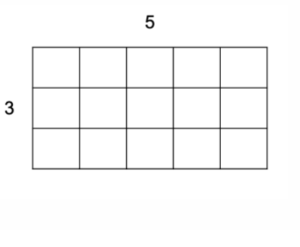
3×10

A student shares the answer 30. When asked “How?” the student answers, “by adding 10+10+10.” After documenting the strategy, the teacher brings the discussion back to the model by pointing to the 3×5 array and asking, “What will the array look like if I’m going to make it represent this problem? Are you imagining what is going to happen?”

Students share that it will get bigger. The teacher then draws the 3×10 array and prompts students to look for the 3×5 array within it, drawing a connection to the previous problem and highlighting doubling.

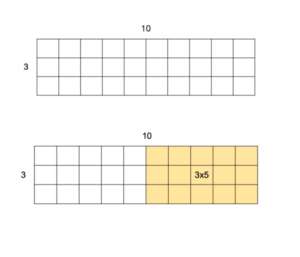
3×11

The teacher cues students to first think about the array: “What would it look like now?” At this point in the lesson, students know that the array has to be bigger, but by how much? With the guidance of a student pointing to the array on the board, the teacher adds another row of 3 to the 3×10 array. A student shares her strategy of multiplying 3×1 and 3×1, which leads to a conversation around place value. “Is the 1 really a 1 or is it a 10?” the teacher asks before using the concrete example of money, ten dollar bills and one dollar bills, to further illustrate this concept. 

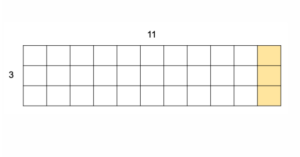
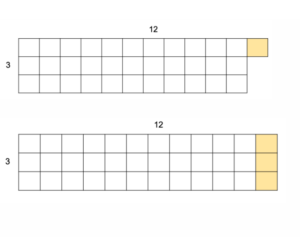
3×12

A student again shares repeated addition, but at this point, repeated addition and skip counting become clumsy strategies as students lose their place or forget their answer. To return to the model and target strategy, the teacher asks, “But, how would we draw it? Are we going to add or take away?” “Add,” students respond. “What are we going to add?” At this point, the group is split. Some say 1 square, getting an answer of 34, and others argue 3, getting an answer of 36. Students turn to their partner to share their ideas. The teacher adds 1 square to the array and asks, “Is it one more?” They think and talk, but the group is still divided, which illustrates a seemingly common misunderstanding that can arise in multiplication number string patterns. Students notice that 12 is 1 more than 11, but are not all making the connection to it being one more group, an important aspect of multiplication and the distributive property. The teacher draws the students’ attention back to the shape of the array with one cube added. “What’s wrong with it?” The students notice that the array is no longer a rectangle so it cannot represent their multiplication problem anymore. Following this explicit guidance from the teacher, the group agrees that they need to add another group of 3. 

References and Resources

Fosnot, C. T., & Dolk, M. (2001). Young mathematicians at work, 2: Constructing
multiplication and division. Heinemann.

Lambert, R., Imm, K., & Williams, D. A. (2017). Number strings: Daily computational fluency.
Teaching Children Mathematics, 24(1), 48–55. Download here.